线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。
线段树可以在 O(log N) 的时间复杂度内实现:
- 单点修改
- 区间修改
- 区间查询(区间求和,求区间最大值,求区间最小值)等操作。
建立线段树
先来看看线段树的结构
假设有一个数组:[10,11,12,13,14],那么建立好的线段树长这样:
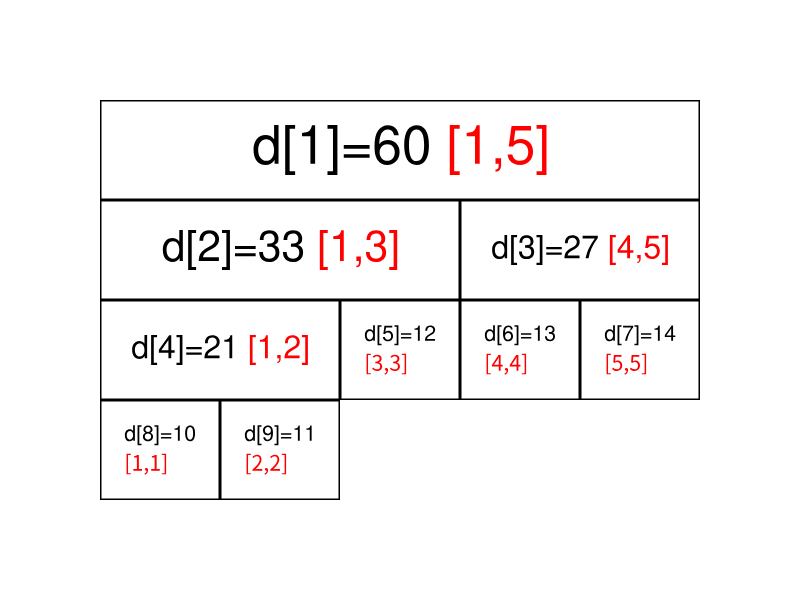
图片来自 OI-wiki
不难写出以下代码:
type SegmentTreeNode struct {
sum int // 负责区间的和
left int // 负责区间左边界
right int // 负责区间右边界
lazy int // 懒标记
}
type SegmentTree struct {
nums []int
tree []*SegmentTreeNode
}
func NewSegmentTree(nums []int) *SegmentTree {
n := len(nums)
st := &SegmentTree{
nums: nums,
tree: make([]*SegmentTreeNode, n*4),
}
st.build(1, 0, n-1)
return st
}
具体地,build 的实现如下:
// 根据给定数组建立线段树
func (st *SegmentTree) build(curNode, left, right int) {
st.tree[curNode] = &SegmentTreeNode{}
st.tree[curNode].left = left
st.tree[curNode].right = right
if left == right {
st.tree[curNode].sum = st.nums[left]
return
}
mid := left + (right-left)/2
st.build(curNode*2, left, mid)
st.build(curNode*2+1, mid+1, right)
st.tree[curNode].sum = st.tree[curNode*2].sum + st.tree[curNode*2+1].sum
}
区间查询
要想查询一个区间的和,我们可以这样做:
- 判断
当前节点负责区间是否为查询区间的子集:- 如果是,那么直接返回区间和即可
- 否则,递归的查询左右子节点
代码实现如下:
// 获取 [left, right] 的和
func (st *SegmentTree) sumRange(curNode, left, right int) int {
node := st.tree[curNode]
// 当前节点的区间为查询区间的子集
if left <= node.left && node.right <= right {
return node.sum
}
// 懒标记下移
st.maintain(curNode)
mid := node.left + (node.right-node.left)/2
res := 0
// 左节点负责区间 [node.left, mid] 与查询区间有交集
if left <= mid {
res += st.sumRange(curNode*2, left, right)
}
// 左节点负责区间 [mid + 1, node.right] 与查询区间有交集
if mid+1 <= right {
res += st.sumRange(curNode*2+1, left, right)
}
return res
}
这里涉及到了一个操作:懒标记下移,我们待会再讲
修改区间
要给区间的每一个数加上一个 offset,如果我们直接依次更新每一个节点,时间复杂度是无法承受的,因此,我们这里引入一个 懒标记 的概念:
- 给区间的每一个数加上一个 offset,不是更新每个节点,而是直接修改 负责这个区间的根节点的 sum,并打上「懒标记」
那「懒」体现在哪里呢?
- 修改时,不会修改每一个节点
- 当后续查询遍历到当前节点时,我们才将修改操作下沉到子节点
文字描述有点抽象,用代码来解释:
// 给 [left, right] 内的数加上 offset
func (st *SegmentTree) update(curNode, left, right, offset int) {
node := st.tree[curNode]
// 当前节点的区间为修改区间的子集
if left <= node.left && node.right <= right {
node.lazy += offset // 打上懒标记
node.sum += (node.right - node.left + 1) * offset
return
}
// 否则,无法直接修改,继续遍历
// 先 maintain 一下
st.maintain(curNode)
mid := node.left + (node.right-node.left)/2
// 左节点负责区间 [node.left, mid] 与查询区间有交集
if left <= mid {
st.update(curNode*2, left, right, offset)
}
// 左节点负责区间 [mid + 1, node.right] 与查询区间有交集
if mid+1 <= right {
st.update(curNode*2+1, left, right, offset)
}
// 更新和
node.sum = st.tree[curNode*2].sum + st.tree[curNode*2+1].sum
}
可以看到,我们并不是直接修改每个节点的值,而是只修改了负责该区间的节点的 sum
懒标记下移
懒标记下移是如何实现的?
每次遍历到某一节点,如果该节点有懒标记,就需要下沉到子节点,具体地:
func (st *SegmentTree) maintain(curNode int) {
node := st.tree[curNode]
if node.lazy == 0 || node.left == node.right { // 不需要懒标记下移
return
}
left := st.tree[curNode*2]
right := st.tree[curNode*2+1]
// 懒标记下移
left.lazy += node.lazy
right.lazy += node.lazy
// 修改左右节点的区间和
left.sum += (left.right - left.left + 1) * node.lazy
right.sum += (right.right - right.left + 1) * node.lazy
node.lazy = 0
}
完整代码
下面给出线段树的模版:
type SegmentTreeNode struct {
sum int // 负责区间的和
left int // 负责区间左边界
right int // 负责区间右边界
lazy int // 懒标记
}
type SegmentTree struct {
nums []int
tree []*SegmentTreeNode
}
func NewSegmentTree(nums []int) *SegmentTree {
n := len(nums)
st := &SegmentTree{
nums: nums,
tree: make([]*SegmentTreeNode, n*4),
}
st.build(1, 0, n-1)
return st
}
func (st *SegmentTree) SumRange(left, right int) int {
return st.sumRange(1, left, right)
}
func (st *SegmentTree) Update(left, right, offset int) {
st.update(1, left, right, offset)
}
func (st *SegmentTree) build(curNode, left, right int) {
st.tree[curNode] = &SegmentTreeNode{}
st.tree[curNode].left = left
st.tree[curNode].right = right
if left == right {
st.tree[curNode].sum = st.nums[left]
return
}
mid := left + (right-left)/2
st.build(curNode*2, left, mid)
st.build(curNode*2+1, mid+1, right)
st.tree[curNode].sum = st.tree[curNode*2].sum + st.tree[curNode*2+1].sum
}
// 获取 [left, right] 的和
func (st *SegmentTree) sumRange(curNode, left, right int) int {
node := st.tree[curNode]
// 当前节点的区间为查询区间的子集
if left <= node.left && node.right <= right {
return node.sum
}
// 懒标记下移
st.maintain(curNode)
mid := node.left + (node.right-node.left)/2
res := 0
// 左节点负责区间 [node.left, mid] 与查询区间有交集
if left <= mid {
res += st.sumRange(curNode*2, left, right)
}
// 左节点负责区间 [mid + 1, node.right] 与查询区间有交集
if mid+1 <= right {
res += st.sumRange(curNode*2+1, left, right)
}
return res
}
// 给 [left, right] 内的数加上 offset
func (st *SegmentTree) update(curNode, left, right, offset int) {
node := st.tree[curNode]
// 当前节点的区间为修改区间的子集
if left <= node.left && node.right <= right {
node.lazy += offset // 打上懒标记
node.sum += (node.right - node.left + 1) * offset
return
}
// 否则,无法直接修改,继续遍历
// 先 maintain 一下
st.maintain(curNode)
mid := node.left + (node.right-node.left)/2
// 左节点负责区间 [node.left, mid] 与查询区间有交集
if left <= mid {
st.update(curNode*2, left, right, offset)
}
// 左节点负责区间 [mid + 1, node.right] 与查询区间有交集
if mid+1 <= right {
st.update(curNode*2+1, left, right, offset)
}
// 更新和
node.sum = st.tree[curNode*2].sum + st.tree[curNode*2+1].sum
}
func (st *SegmentTree) maintain(curNode int) {
node := st.tree[curNode]
if node.lazy == 0 || node.left == node.right { // 不需要懒标记下移
return
}
left := st.tree[curNode*2]
right := st.tree[curNode*2+1]
// 懒标记下移
left.lazy += node.lazy
right.lazy += node.lazy
// 修改左右节点的区间和
left.sum += (left.right - left.left + 1) * node.lazy
right.sum += (right.right - right.left + 1) * node.lazy
node.lazy = 0
}